我們昨天討論了批次處理和Momentum，並解釋了如何藉由考慮過去的梯度下降來決定模型訓練的前進方向，這種方式能幫助我們在模型訓練時跨越一些Critical Point，如鞍點（saddle point）和局部極小值（local minima）。然而，在訓練過程中，我們有時可能會遇到這樣的情況：並非卡在鞍點或局部極小值，但損失函數（loss）仍無法繼續下降。這時該怎麼辦呢？今天要介紹的幾種算法，正是為了解決這類問題而設計的工具。

其中一種方法叫做AdaGrad。簡單來説，AdaGrad就是一個可以動態的調整Learning Rate的一個演算法，我們先來看原本的gradient decent在設置learning rate的時候，太大或太小會怎麽樣：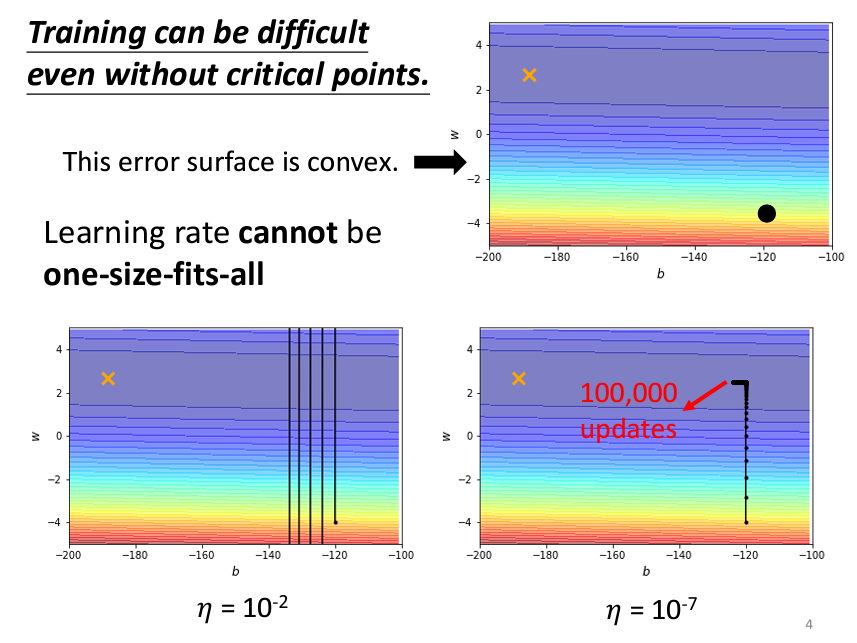

可以看到，如果learning rate設置太大的話，我的Loss可能會有很大的震蕩并且到不了我的理想的目標值；而設太小的話，哪怕迭代很多次，也到不了我們的目標值。因此可以看出，我們需要在不同的情況下，根據每個參數設置不同的learning rate。

Learning Rate設置

至於這個learning rate要怎麽設置呢？我們可以想象一下，如果今天在一個平原，和在一個陡峭的懸崖旁邊，你是不是就會在平原上走的快一些，在懸崖旁邊走的慢一些，這一點用在gradient decent也是一樣。我們先來看標准的gradient decent：

而我們現在做的，就是讓這個gradient decent的每一次更新都depent on一個parameter σ：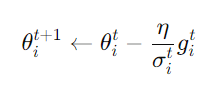

各種Learning Rate的調整方法

Root Mean Square

簡單來説，σ就是考慮了之前所有的gradient，將他們取平均再開根號，來讓我們動態的去計算不同情況下的learning rate，具體方程式如下：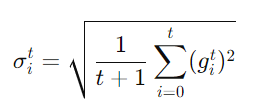

這一個演算法被運用在AdaGrad裏面，但是這個演算法并不是最後的版本（還能繼續推演），因爲哪怕是同一個參數，它的error surface也可能會在不同的時候需要不同的learning rate：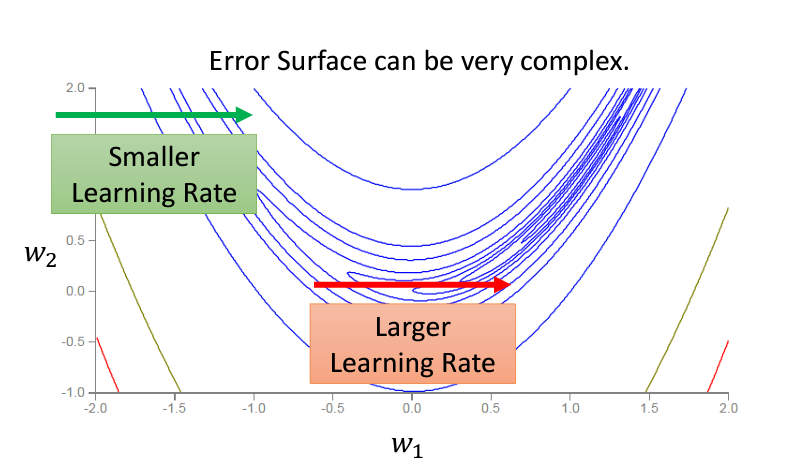

因此我們還需要一個新的招數，叫做RMSProp。

RMSProp

這個RMSProp就是基於Root Mean Square的延申，剛剛的Root Mean Square對於所有的gradient都有同等的重要性（因爲是1/t+1），但是在RMSProp裏面，我們可以自己調整現在的gradient有多重要。具體怎麽樣調整呢？我們通過一個hyper parameterα來進行調整：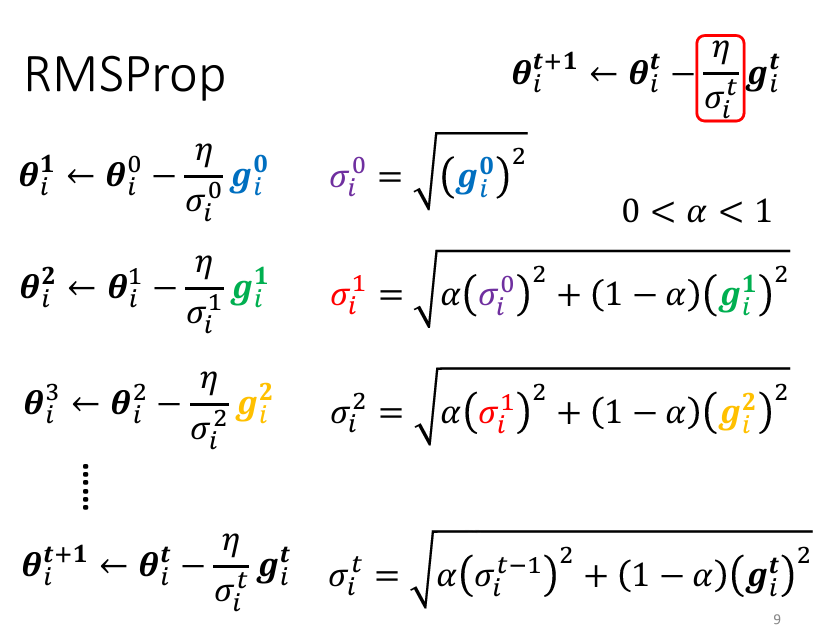

如果説我今天把α設的很小（趨近於0），就表示我在當前的位置的gradient相較於之前的gradient的和比較重要，反之（趨近於1）亦然。這個RMSProp會比上面的Root Mean Square反應來的快，當遇到比較大的gradient的時候能夠及時刹車。我們常用的Optimizer裏面的Adam就是使用了RMSProp + Momentum的方式得出來的策略。

Learning Rate Scheduling

Learning Rate Scheduling是説我們的學習率etaη要跟時間有關聯，以下是常見的策略：

Learning Rate Decay

隨著時間（參數不斷update），我們讓這個η越來越小，爲什麽要這樣呢？因爲我們假設一開始離目標很遠，所以我們的步伐可以邁大步一點，但是隨著我們的參數更新後，我們會越來越靠近我們的目標，因此我們要越走越慢，來緩慢靠近我們的目標。

Warm Up

另外一種方法叫做warm up，意思是我們的learning rate要先變大，後變小。這個方法在許多的論文和模型很常出現，如Bert，ResNet，Transformer等。


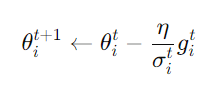
這個方法的意思是說，當我們在更新我們的參數的時候，會計算sigmaσ，而這個sigma是一個統計的結果，因爲是統計的結果，所以要看比較多筆數據以後才精準，所以一開始把learning rate設大一點，就可以讓我們的參數變化在一開始的時候不會跨太大步，先探索一下附近的地形的概念。

以上的内容來自於臺大教授李宏毅：鏈接，我只是把他的影片寫成了筆記。